La trampa de las proyecciones ARIMA convergentes (MARTIN, J.M.)

Mg. José-Manuel Martin Coronado
Chief Economist - EMECEP Consultoría
Lima, 10 de julio de 2019

Los modelos ARIMA(p,d,0) se basan en procesos iterativos de estimación que buscan minimizar el valor absoluto del logaritmo del indice de verosimilitud a través de la estimación de un coeficiente de correlación común entre los rezagos de la variable elegida. La versión más simple son los modelos AR (d=0) y los modelos ARI (d=1), mientras que los modelos ARIMA completos requieren la estimación de un parámetro que relaciona a los errores en el tiempo a través de medias móviles (q). 

En el caso más sencillo, un modelo MCO autoregresivo de orden uno es: Y_t = Bo + B1*Y_t-1 + U_t, mientras que un modelo ARIMA(1,0,0) sería Y_t - pY_t-1 = Ao (1-p) + U_t. Si se reordena la ecuación: Y_t = Ao(1-p) + pY_t-1 + U_t = Bo + B1*Y_t-1 + U_t. Por el momento se asume que los errores son similares. Esta especificación permite deducir que Bo = Ao(1-p) y B1 = p. Por ejemplo, si Bo = 315.2299,  Ao = 931.7154 y p = 0.6646127, entonces Ao*(1-p) = 312.48. La diferencia sería no significativa. 

Si bien las diferencias entre estimación MCO y ML pueden incrementarse según el modelo elegido, el aspecto que será de interés para este artículo es la utilidad de estos modelos para elaborar proyecciones econométricas. Como se recordará, si se trata de modelos univariantes, es posible realizar proyecciones de la variable elegida con mayor facilidad que si se tratara de un modelo multivariante. Es así que simplemente con un rezago es posible realizar proyecciones en horizontes más largos, tales como 6 meses o 12 meses. 

Ahora bien, ello es matematicamente posible, aunque no necesariamente recomendable. Es decir, si se tienen muy pocos datos en la muestra, no es recomendable utilizarlo para proyectar un horizonte similar o mayor al de la muestra. Asumiendo que el/la modelador/a es suficientemente diligente para no excederse en las propiedades de las proyecciones ARIMA, aún así es posible que se encuentre con el problema de las proyecciones convergentes. 

En concreto existen tres tipos básicos de proyecciones ó mejor dicho de resultados de proyecciones. 1) Convergentes, 2) Divergentes y 3) Espectrales. Las primeras presentan una trayectoria notoramiente encaminada a un valor de convergencia final. Las segundas en cambio muestran que conforme se llega al final del horizonte de proyección, los valores finales son cada vez más volátiles  y/o alejados a los inicialmente concebidos. Finalmente, las proyecciones espectrales tienen un comportamiento que no coincide con los dos primeros, sino con la última evolución registrada por el modelador, por ejemplo, el comportamiento similar al de los últimos 12 meses. 

Particularmente, las proyecciones convergentes sugieren al modelador que la trayectoria de la serie podría llegar a un estado estacionario, el cual tiene un interés especial, por su interpretación como valor óptimo o valor de largo plazo. Aunque esto no debería confundirse con las funciones de transferencia que permiten obtener las relaciones de largo plazo. Por el contrario, el valor de convergencia puede representar un valor de equilibrio deseado por el modelador, el cual a su criterio, podrían interpretarse como una autovalidación del modelo elaborado.

Una de las causas de la aparición de proyecciones convergentes es la existencia de modelos ARIMA de órden inferior al "óptimo". El problema radica en que los órdenes inferiores podrían ser correctos estadísticamente (estables, eliminan la aucorrelación, estacionarios) pero tener un resultado poco realista, por ejemplo una convergencia hacia un valor promedio o intercepto. Una manera de evitar ello es agregando más rezagos al modelo ARIMA, de modo que absorba de una mejor manera el comportamiento anualizado de la variable elegida, aunque con un costo en la significancia individual.

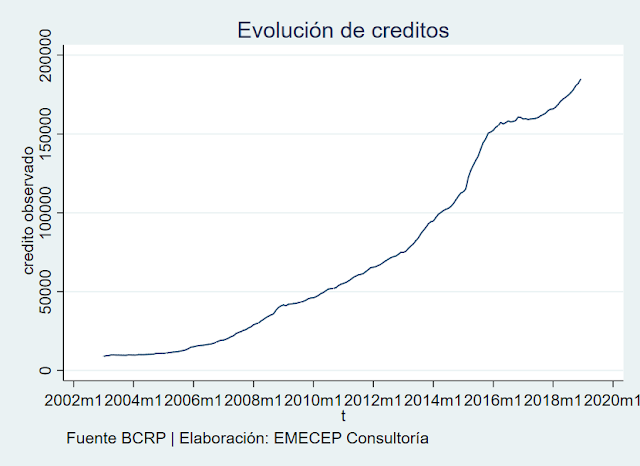
A fin de verificar estas ideas, se realizó una simulación en STATA15, con una variable de interés: Los creditos del sistema financiero peruano. Dicha variable se observa que no es estacionaria por lo que no se recomienda realizar un modelo ARIMA(p,0,q), es decir en niveles, dado que existe un alto riesgo de no convergencia en el proceso iterativo, lo cual no ocurriría si se estimara mediante un MCO. Incluso, una proyección tendencial podría sugerir un crecimiento exponencial y divergente de esta variable.

Se probaron modelos ARIMA(p,1,0) con valores de p=1 a 12, por tratarse de data mensual. Así mismo, cada uno de estos modelos ARIMA se utilizaron para hacer proyecciones a 12 meses de la variable créditos, es decir todo el 2019. Debe recordarse que la convergencia se observará más claramente en la variable endógena de los modelos ARIMA, en este caso, la diferencia de los créditos, es decir:

Puede observarse que los dos primeros modelos arima revelan la convergencia antes indicada, aproximadamente en un valor cercano a 900. En realidad, ese valor es compatible con el promedio de la variable endógena (919.711) y/o el intercepto de dichos modelos (Aprox 940). No obstante, conforme se insertan más rezagos se observa que la proyección se vuelve ligeramente más espectral aunque sin llegar a serlo del todo, pues mantiene una tendencia ligeramente volatil decreciente.  

Esto permite además que la proyección de la variable en niveles (obtenida a partir de la suma acumulada de la endógena estimada sea a su vez convergente hacia un valor determinado. 

Cabe precisar que al estacionarizar los créditos a través de las diferencias no se logró eliminar el promedio de dicha variable, es decir, la media de dicha variable endógena no es cero. Y es por ello que la convergencia observada no es tan rápida como en otros casos. En efecto, si la media de la variable fuera cero, la trampa de la convergencia sería aún más notoria, por ejemplo si se tomara la serie en logaritmos y/o en segundas diferencias. Cabe precisar que la transformaciones asimétricas, tales como los logaritmos son menos preferibles a las simétricas como lo son las primeras o segundas diferencias. 

Tal como se puede observar en el último gráfico, la técnica de los logaritmos invierte la trayectoria de convergencia de un ritmo negativo decreciente a uno positivo descreciente, cuyos primeros valores rezagados arriba rápidamente a una convergencia, a diferencia del modelo sin transformación logaritmica. En tal sentido, sería poco realista utilizar logaritmos y diferencias en un modelo de orden autoregresivo de orden 1 o 2, por cuanto asumiría que los valores proyectados no cambian en el tiempo en diferencias, con lo cual los valores en niveles serían casi constantes. 

En conclusión, es necesario tener mucho cuidado al realizar proyecciones con modelos ARIMA. Si bien el modelo con uno o pocos rezagos pueden ser estadísticamente atractivo para estimación, no necesariamente lo es para la proyección. Resulta necesario utilizar una cantidad suficiente de rezagos (12 si es mensual, 4 si es trimestral, por ejemplo) a pesar que la significancia individual de algunos coeficientes de correlación caiga, si ello no altera la bondad de ajuste del modelo, ni el realismo económico del mismo, entonces se trataría de una opción viable. 

Además, en los casos simulados se han utilizado modelos ARIMA completos, lo cual no es un requisito esencial, ya podría haberse tomado 1, 3 y 12 rezagos solamente, a fin de obtener un modelo que combine las buenas propiedades de estimación y de proyección. Y como puede confirmarse, dependiendo del modelo elegido, la diferencia entre un ARIMA completo y uno incompleto serìa no significativa, sobre todo coincidirìan en la ausencia de la convergencia artificial discutida. En concreto, a veces es mejor un modelo ARIMA incompleto con muchos rezagos (hasta 12 si es mensual) que uno modelo ARIMA completo con muy pocos rezagos