Impactos no lineales de la multicolinealidad sobre la eficiencia de los estimadores [MARTIN C., J.M.]
José-Manuel Martin Coronado
Chief Economist EMECEP Consultoría
Prof. Investigador, Instituto Econometría de Lima
La literatura econométrica reconoce que la existencia de multicolinealidad se relaciona con el problema de la ineficiencia, en el sentido que genera una inflación en la varianza de los estimadores. No obstante, ya se ha indicado que la multicolinealidad por sí misma no necesariamente es algo negativo, dado que es complicado encontrar regresores ortogonales. El problema estará cuando esta redundancia sea extrema y, peor aún, estas variables no reduzcan significativamente la varianza del error. Ahora bien, la relación en cuestión, como es usual, se asume que es lineal negativa, mal llamada "inversa", lo cual asume que existen cambios marginales constante sin embargo, como se verá a continuación, en el fondo podrían ocurrir cambios marginales no constantes, es decir, una relación no lineal.
En términos matriciales se trata de la siguiente expresión: Var(B) = σ2(X'X)-1= e'e.(N-K)-1(X'X)-1. No obstante, esta fórmula no es precisa en definir cuál es la varianza de cada uno de los estimadores ó por lo menos de aquellos que sean de interés. Así, matricialmente se sabe que el determinante de la matriz X'X juega un rol fundamental. Debe recordarse que esta matriz también se le conoce como la suma de los cuadrados de los regresores y alberga a la matriz de varianzas y covarianzas de las variables. Así, si se incrementa los elementos resultantes de la división entre la adjunta de dicha matriz y su determinante, se generará mayores valores de los elementos de la inversa, lo cual implicará mayores valores la varianza de los estimadores, los cuales pueden o no ser contrarrestados por la caída en la varianza de los residuos. Y dicho determinante no sólo depende de la diagonal principal de la matriz X'X sino también de los elementos simétricos que pueden disminuir dicho determinante, los cuales contienen a la covarianza entre las variables explicativas.
Otro enfoque estadístico (usualmente más directo y legible) reorganiza e individualiza la varianza de los betas, en particular aquella de la segunda variable de un modelo multivariable. En otras palabras, si el modelo inicial es Y = B0 + B1X1 + u1, y se desea evaluar la eficiencia del estimador de una nueva variable X2, es decir Var(B2), cuya fórmula no necesariamente es Varbiv(B2) = σ2(X2'X2)-1 = σ2{Σ[X2-E(X2)]2}-1 = σ2SCT2-1 debido a la interacción que puede existir entre X2 y X1 (o entre ésta y las variables incumbentes, de ser el caso) . La fórmula en cuestión depende de una regresión auxiliar dada por X2 = A0 + A1X1 + u2, de la cual se extrae la Suma de los Cuadrados de los Residuos (SCR2), que equivale a SCT2(1-R22) y que Var(X2) = σ22 = SCT2/(n-1) . Por lo tanto la fórmula debe ajustarse desde un enfoque multivariante a Varmult(B2) = σ2/[SCT2(1-R22)] = σ2{Σ[X2-E(X2)]2}-1(1-R22)-1= σ2{(n-1)σ22}-1(1-R22)-1. Nótese que esto también puede replicarse para X1, es decir Varmult(B1) = σ2{(n-1)σ12}-1(1-R12)-1 . Esta fórmula permite deducir que si no existe relación entre dicha variable y las demás variables incumbentes (en este caso X1) el R22 será cero ó casi cero, con lo cual la varianza multivariable del estimador será igual que la varianza bivariable del mismo, sobre todo si no llega a aportar a la reducción significativa de la varianza del residuo.
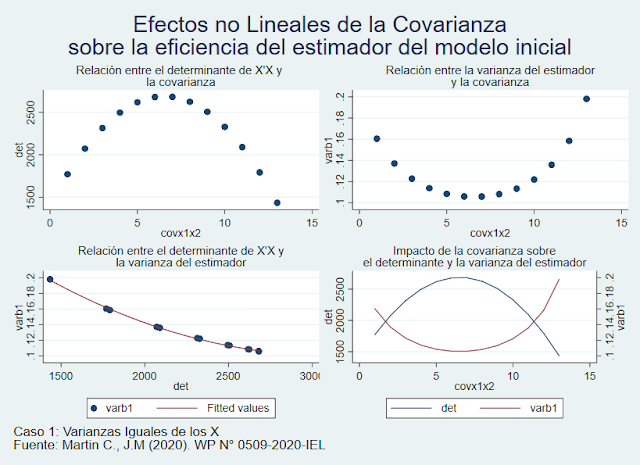
Estos dos enfoques son complementarios. Sin embargo, tal vez algunas imágenes valen más que mil palabras (o fórmulas). Así mismo, las imágenes a presentarse, revelarán algo que las formulas no sugieren a simple vista. Para ello, partiremos de una matriz X'X de un modelo Y = (1 X1 X2)B tal que N=30, ΣX1 = ΣX2 = 14 y , ΣX12 = ΣX22 = 15 (Proxy de las varianzas), ΣX1X2 = 1 (Proxy de covarianza), e'e=1 y que ΔGL= - Δe'e. De modo tal que la matriz X'X es [30 14 14, 14 15 1 , 14 1 15]. Nótese que el segundo momento de las variables es ligeramente superior al primer momento (aunque todas iguales entre X1 y X2), lo cual sugiere que las varianzas en este caso son pequeñas. El ejercicio en este caso consiste en incrementar progresivamente la covarianza para observar el impacto en el determinante de la matriz X'X que a su vez afectará a los elementos de la inversa y, finalmente, sobre la varianza de B1. Se prefiere un análisis sobre la variable incumbente pues en este ejercicio se busca discutir la inclusión o no de la variable X2, en función del impacto favorable o no sobre el modelo inicial. Los resultados se presentan a continuación.
Nótese que en este primer caso, las varianzas de las variables son iguales, un supuesto que será cambiando en los siguientes gráficos. No obstante, se puede observa la no linealidad del impacto de una mayor covarianza tanto en el determinante como en la eficiencia del estimador de la variable incumbente. Así mismo, la relación entre determinante y varianza de dicho estimador es de tipo inversa, y no del tipo lineal negativa, lo cual se confirma con una regresión no lineal para este caso. Este gráfico entonces permite sugerir que un poco de multicolinealidad es buena, sobre todo si aporta algo de explicatividad, pero en exceso genera un impacto importante e incluso, como se sabe, la imposibilidad de estimar el modelo (determinante negativo, problema de rango, entre otros).
Resulta interesante notar que si la varianza de X2 es menor (13) a la varianza de X1 (16) el impacto sobre la varianza de B1 no sólo será mayor sino que también será aún más pronunciado en la parte creciente y menos pronunciado en la parte decreciente. Por el contrario, si la varianza de X2 fuera mayor (19) a la varianza de X1 (16) la curvatura de la función sería más homogénea ó balanceada y los valores, además que la varianza del estimador B1 se reduce.
Esto quiere decir que el efecto sería prácticamente opuesto, aunque ello no cambia la relación no linealidad obtenida. Incluso si se cambian algunos parámetros, habida cuenta que no generen determinante cero o negativo, podrán existir giros ó asimetrías como las observadas en lo casos 2 y 3, pero del mismo modo se mantendrá el impacto no lineal de la multicolinealidad sobre la eficiencia de los estimadores, conforme se observa en el último gráfico.
Lima, 09 de mayo de 2020.
En términos matriciales se trata de la siguiente expresión: Var(B) = σ2(X'X)-1= e'e.(N-K)-1(X'X)-1. No obstante, esta fórmula no es precisa en definir cuál es la varianza de cada uno de los estimadores ó por lo menos de aquellos que sean de interés. Así, matricialmente se sabe que el determinante de la matriz X'X juega un rol fundamental. Debe recordarse que esta matriz también se le conoce como la suma de los cuadrados de los regresores y alberga a la matriz de varianzas y covarianzas de las variables. Así, si se incrementa los elementos resultantes de la división entre la adjunta de dicha matriz y su determinante, se generará mayores valores de los elementos de la inversa, lo cual implicará mayores valores la varianza de los estimadores, los cuales pueden o no ser contrarrestados por la caída en la varianza de los residuos. Y dicho determinante no sólo depende de la diagonal principal de la matriz X'X sino también de los elementos simétricos que pueden disminuir dicho determinante, los cuales contienen a la covarianza entre las variables explicativas.
Otro enfoque estadístico (usualmente más directo y legible) reorganiza e individualiza la varianza de los betas, en particular aquella de la segunda variable de un modelo multivariable. En otras palabras, si el modelo inicial es Y = B0 + B1X1 + u1, y se desea evaluar la eficiencia del estimador de una nueva variable X2, es decir Var(B2), cuya fórmula no necesariamente es Varbiv(B2) = σ2(X2'X2)-1 = σ2{Σ[X2-E(X2)]2}-1 = σ2SCT2-1 debido a la interacción que puede existir entre X2 y X1 (o entre ésta y las variables incumbentes, de ser el caso) . La fórmula en cuestión depende de una regresión auxiliar dada por X2 = A0 + A1X1 + u2, de la cual se extrae la Suma de los Cuadrados de los Residuos (SCR2), que equivale a SCT2(1-R22) y que Var(X2) = σ22 = SCT2/(n-1) . Por lo tanto la fórmula debe ajustarse desde un enfoque multivariante a Varmult(B2) = σ2/[SCT2(1-R22)] = σ2{Σ[X2-E(X2)]2}-1(1-R22)-1= σ2{(n-1)σ22}-1(1-R22)-1. Nótese que esto también puede replicarse para X1, es decir Varmult(B1) = σ2{(n-1)σ12}-1(1-R12)-1 . Esta fórmula permite deducir que si no existe relación entre dicha variable y las demás variables incumbentes (en este caso X1) el R22 será cero ó casi cero, con lo cual la varianza multivariable del estimador será igual que la varianza bivariable del mismo, sobre todo si no llega a aportar a la reducción significativa de la varianza del residuo.
Estos dos enfoques son complementarios. Sin embargo, tal vez algunas imágenes valen más que mil palabras (o fórmulas). Así mismo, las imágenes a presentarse, revelarán algo que las formulas no sugieren a simple vista. Para ello, partiremos de una matriz X'X de un modelo Y = (1 X1 X2)B tal que N=30, ΣX1 = ΣX2 = 14 y , ΣX12 = ΣX22 = 15 (Proxy de las varianzas), ΣX1X2 = 1 (Proxy de covarianza), e'e=1 y que ΔGL= - Δe'e. De modo tal que la matriz X'X es [30 14 14, 14 15 1 , 14 1 15]. Nótese que el segundo momento de las variables es ligeramente superior al primer momento (aunque todas iguales entre X1 y X2), lo cual sugiere que las varianzas en este caso son pequeñas. El ejercicio en este caso consiste en incrementar progresivamente la covarianza para observar el impacto en el determinante de la matriz X'X que a su vez afectará a los elementos de la inversa y, finalmente, sobre la varianza de B1. Se prefiere un análisis sobre la variable incumbente pues en este ejercicio se busca discutir la inclusión o no de la variable X2, en función del impacto favorable o no sobre el modelo inicial. Los resultados se presentan a continuación.
Resulta interesante notar que si la varianza de X2 es menor (13) a la varianza de X1 (16) el impacto sobre la varianza de B1 no sólo será mayor sino que también será aún más pronunciado en la parte creciente y menos pronunciado en la parte decreciente. Por el contrario, si la varianza de X2 fuera mayor (19) a la varianza de X1 (16) la curvatura de la función sería más homogénea ó balanceada y los valores, además que la varianza del estimador B1 se reduce.
Esto quiere decir que el efecto sería prácticamente opuesto, aunque ello no cambia la relación no linealidad obtenida. Incluso si se cambian algunos parámetros, habida cuenta que no generen determinante cero o negativo, podrán existir giros ó asimetrías como las observadas en lo casos 2 y 3, pero del mismo modo se mantendrá el impacto no lineal de la multicolinealidad sobre la eficiencia de los estimadores, conforme se observa en el último gráfico.
Lima, 09 de mayo de 2020.



Comments
Post a Comment