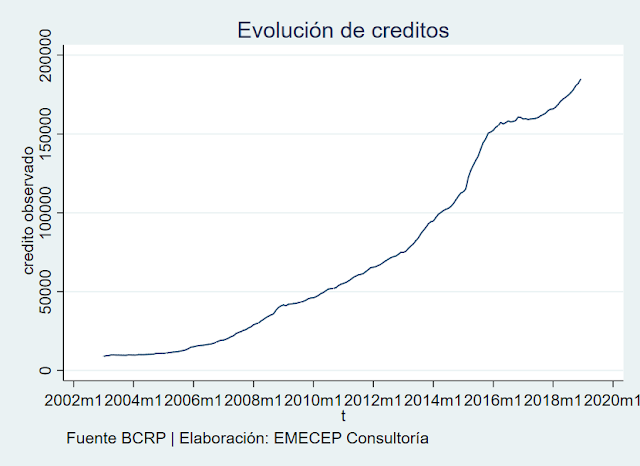
¿Y cómo se trabaja con un modelo ARIMA de medias móviles? [MARTIN, JM]

Mg. José-Manuel Martin Coronado Chief Economist, EMECEP Consultoría www.emecep-consultoria.com Docente Principal, Instituto de Econometría de Lima www.institutoeconometria.com www.martineconometrics.com Lima, 29 de julio de 2019 1.- Introducción El tratamiento de la autocorrelación es uno de los aspectos fundamentales de la econometría. Más allá de que tenga que ser un supuesto MCO, la autocorrelación de los errores genera ineficiencia en los parámetros estimados y por lo tanto un mayor error en la variable endógena estimada. Por ello, su tratamiento es prioritario. Ahora bien, esto plantea una interrogante: ¿Qué tipo de modelamiento y/o método de estimación es el más recomendable? Muchos dirán automáticamente que debe hacerse un SARIMA, pero antes de ello, debe analizarse la naturaleza de la serie de tiempo y verificar si efectivamente requiere hacerse un modelo con esas propiedades o tal vez uno más simple que cumpla con el cometido. En el presente artíc...